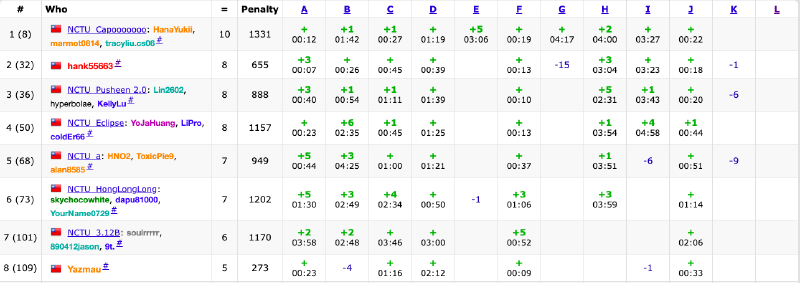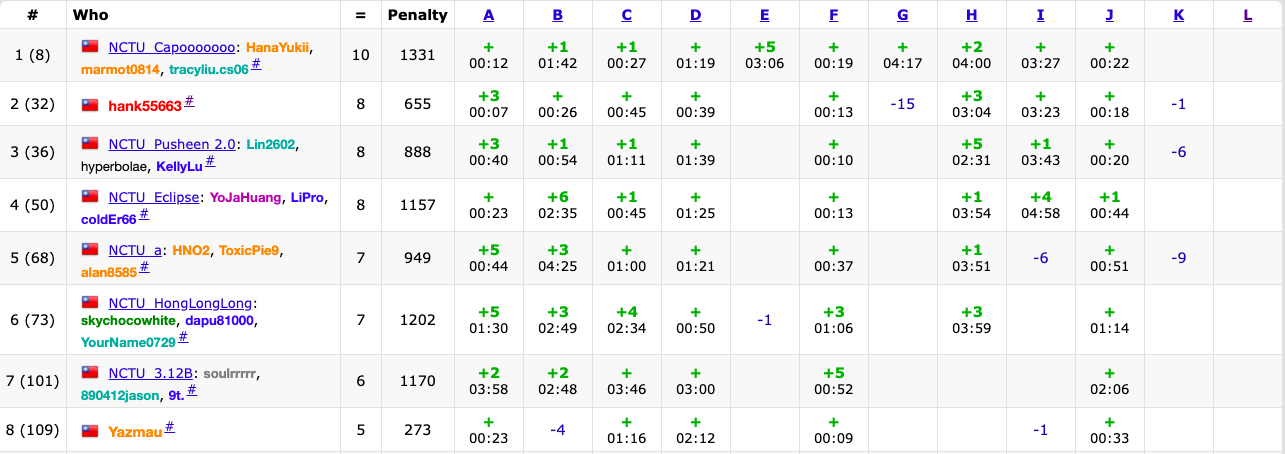
pA
- 問題:2 <= n <= 1e18,2 <= k <= 1e12,求 n! 是 k 的幾次方。
- 作法:將 k 做質因數分解,然後各自算出次方數後,再取最小值。
- 時間:$$O(\log n \sqrt k)$$
1#include<bits/stdc++.h>
2using namespace std;
3typedef long long ll;
4typedef pair<ll, int> pli;
5vector<pli> prime_factor (ll k) {
6 vector<pli> ret;
7 for (ll i = 2; i * i <= k; i++) {
8 if (k % i) continue;
9 pli p = pli(i, 0);
10 while (k % i == 0) k /= i, p.second++;
11 ret.push_back(p);
12 }
13 if (k > 1) ret.push_back(pli(k ,1));
14 return ret;
15}
16int main() {
17 ios_base::sync_with_stdio(0); cin.tie(0);
18 int T; cin >> T;
19 while (T--) {
20 ll n, k, ans = -1; cin >> n >> k;
21 vector<pli> fac = prime_factor(k);
22 for (pli p : fac) {
23 ll cnt = 0, m = n;
24 while (m) cnt += (m = m / p.first);
25 cnt /= p.second;
26 if (ans == -1 || cnt < ans) ans = cnt;
27 } cout << ans << "\n";
28 } return 0;
29}
pB
- 問題:給定兩個相同長度的字串,問能不能各自找到長度至少一半的子字串,使得字元和字元兩兩的絕對值差不超過 1。例如 “aabb” 和 “bbbb” 就是符合的。
- 作法:平移後,對重疊處做最大連續和。
- 時間:$$O(n^2)$$
1#include<bits/stdc++.h>
2using namespace std;
3int main() {
4 ios_base::sync_with_stdio(0); cin.tie(0);
5 int T; cin >> T;
6 while (T--) {
7 int n; cin >> n;
8 string a, b; cin >> a >> b;
9 int ans = 0;
10 for (int i = 0; i < n; i++) {
11 for (int j = 0, sum = 0; j + i < n; j++)
12 if (abs(a[j] - b[j + i]) <= 1)
13 ans = max(ans, ++sum);
14 else sum = 0;
15 for (int j = 0, sum = 0; j + i < n; j++)
16 if (abs(a[j + i] - b[j]) <= 1)
17 ans = max(ans, ++sum);
18 else sum = 0;
19 }
20 if (ans * 2 >= n) cout << "POSITIVE\n";
21 else cout << "NEGATIVE\n";
22 }
23 return 0;
24}
pC
pD
pE
pF
pG
pH
pI
pJ
pK
- Coloring on Plannar Graph
pL