AtCoder Beginning Contest 192
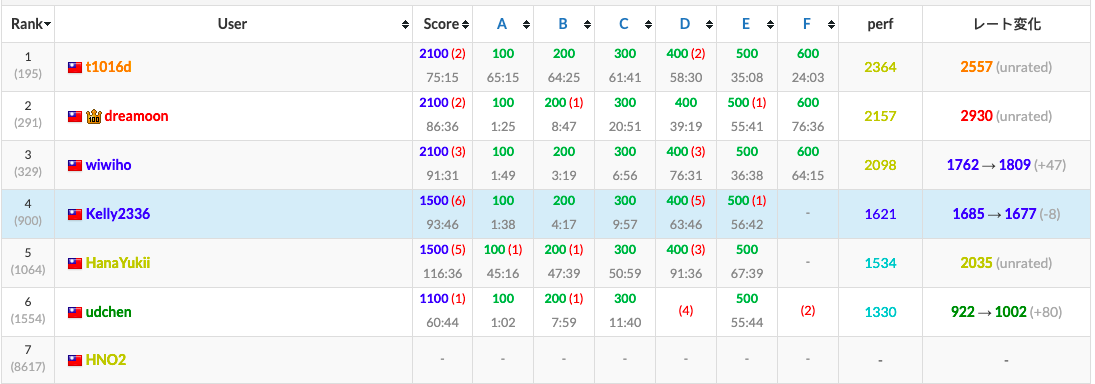
pD 被卡了很久,pF 沒靈感,只好掉分。
A. Star
$$O(1)$$
1#pragma GCC optimization ("O3")
2#include<bits/stdc++.h>
3using namespace std;
4int main() {
5 ios::sync_with_stdio(0), cin.tie(0);
6 int x; cin >> x;
7 cout << 100 - x % 100 << "\n";
8 return 0;
9}B. uNrEaDaBlE sTrInG
$$O(|S|)$$
1#pragma GCC optimization ("O3")
2#include<bits/stdc++.h>
3using namespace std;
4int main() {
5 ios::sync_with_stdio(0), cin.tie(0);
6 string s;
7 cin >> s;
8 int len = s.length();
9 bool check = true;
10 for (int i = 0; i < len; i += 2)
11 if (isupper(s[i]))
12 check = false;
13 for (int i = 1; i < len; i += 2)
14 if (islower(s[i]))
15 check = false;
16 if (check) cout << "Yes\n";
17 else cout << "No\n";
18 return 0;
19}C. Kaprekar Number
$$O(K \log N)$$
1#pragma GCC optimization ("O3")
2#include<bits/stdc++.h>
3using namespace std;
4#define pb push_back
5int f(int x) {
6 vector<int> v;
7 while (x) {
8 v.pb(x % 10);
9 x /= 10;
10 }
11 sort(v.begin(), v.end());
12 int g1 = 0, g2 = 0;
13 for (int i = v.size() - 1; i >= 0; i--)
14 g1 = g1 * 10 + v[i];
15 for (int i = 0; i < v.size(); i++)
16 g2 = g2 * 10 + v[i];
17 return g1 - g2;
18}
19int main() {
20 ios::sync_with_stdio(0), cin.tie(0);
21 int n, k; cin >> n >> k;
22 while (k--) n = f(n);
23 cout << n << "\n";
24 return 0;
25}D. Base n
- 因為 int64 裝不下,就直接開 python 寫了,下次應該會用
__int128_t。 - 解法:二分搜,但 X 長度為 1 的時候要特判。
- 被卡了很久,這場的大敗筆 QAQ
$$O(|X| \log M)$$
1s = input()
2m = int(input())
3d = 0
4for c in s:
5 d = max(d, int(c))
6low = d + 1
7high = 1000000000000000000
8ans = d
9if len(s) <= 1:
10 if int(s) <= m:
11 print(1)
12 else:
13 print(0)
14else:
15 while low <= high:
16 mid = (low + high) // 2
17 cnt = 0
18 for c in s:
19 cnt = cnt * mid + int(c)
20 if cnt <= m:
21 ans = mid
22 low = mid + 1
23 else:
24 high = mid - 1
25 print(ans - d)E. Train
- 解法:最短路徑 Dijkstra。
- 被 Long Long Int 卡了一下 QQ
$$O(M \log N)$$
1#pragma GCC optimization ("O3")
2#include<bits/stdc++.h>
3using namespace std;
4typedef long long ll;
5typedef pair<ll, int> pii;
6#define pb push_back
7struct edge {
8 int to, t, k;
9 edge(int _to, int _t, int _k) {
10 to = _to, t = _t, k = _k;
11 }
12};
13int main() {
14 ios::sync_with_stdio(0), cin.tie(0);
15 int n, m, x, y;
16 cin >> n >> m >> x >> y;
17 vector<vector<edge> > G(n + 1);
18 for (int i = 0; i < m; i++) {
19 int a, b, t, k;
20 cin >> a >> b >> t >> k;
21 G[a].pb(edge(b, t, k));
22 G[b].pb(edge(a, t, k));
23 }
24 vector<ll> dis(n + 1, -1);
25 priority_queue<pii, vector<pii>, greater<pii> > pq;
26 dis[x] = 0;
27 pq.push({dis[x], x});
28 while (!pq.empty()) {
29 int u = pq.top().second; pq.pop();
30 if (u == y) break;
31 for (edge e : G[u]) {
32 ll time = dis[u];
33 if (time % e.k) time += e.k - time % e.k;
34 if (dis[e.to] == -1 || dis[e.to] > time + e.t) {
35 dis[e.to] = time + e.t;
36 pq.push({dis[e.to], e.to});
37 }
38 }
39 }
40 cout << dis[y] << "\n";
41 return 0;
42}F. Potion
- 看了 Dreamoon 的講解才想到要怎麼設 DP 狀態,覺得這題是可想出來的難度。
- 題意:給定 N ≤ 100 個數字 ≤ 1e7,將 k 個數字融合的分數為他們的和,另外每天會增加 k,且只能在第 0 天融合。給定一個數字 1e9 ≤ X ≤ 1e18,問最少要多少天才能湊到剛好 X 的分數。
- 解法:對於每個 k 都求 DP[i][j] 以 i 個數字和模 j 的最大值。
$$O(N^4)$$
1#pragma GCC optimization ("O3")
2#include<bits/stdc++.h>
3using namespace std;
4typedef long long ll;
5int main() {
6 ios::sync_with_stdio(0), cin.tie(0);
7 int n;
8 ll x;
9 cin >> n >> x;
10 vector<int> a(n);
11 for (int i = 0; i < n; i++) cin >> a[i];
12 ll ans = x;
13 for (int k = 1; k <= n; k++) {
14 ll dp[100][100] = {};
15 for (int x : a) {
16 for (int i = k; i >= 1; i--) {
17 for (int j = 0; j < k; j++) {
18 if (dp[i - 1][j] % k != j) continue;
19 if (!dp[i - 1][j] && i > 1) continue;
20 int r = (j + x) % k;
21 dp[i][r] = max(dp[i][r], dp[i - 1][j] + x);
22 }
23 }
24 }
25 if (dp[k][x % k] && (x - dp[k][x % k]) % k == 0)
26 ans = min(ans, (x - dp[k][x % k]) / k);
27 }
28 cout << ans << "\n";
29 return 0;
30}